Sirkelbevegelse

Konstant banefart

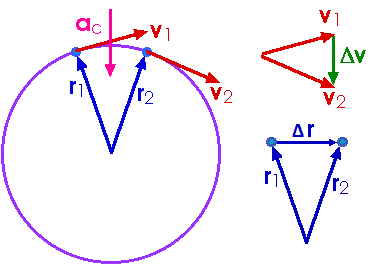
Vi skal først sjå på sirkelbevegelse med konstant banefart. Figuren under viser fartsvektorane og posisjonsvektorane i to punkt. Det at bevegelsen går i sirkel betyr at lengden av radien er konstant, dvs. |r₁| = |r₂| , og det at banefarten er konstant betyr at absoluttverdien av fartsvektoren også er konstant, dvs.  |v₁| = |v₂|. Det er med andre ord bare retningen på fartsvektoren som endrar seg.

Vi skal no finna eit uttrykk for akselerasjonen, og bruker då definisjonen:

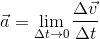
Fartsvektoren er alltid ein tangent til banen. For sirkelbevegelse betyr det at vektoren v står normalt på vektoren r. Det betyr igjen at vi har samme vinkel θ mellom  vektorane r₁ og r₂ som vi har mellom v₁ og v₂. Vi har derfor to likebeina trekanter som er likeforma. For å visa dette tydeligare er disse to trekantane tegna kvar for seg til høgre på figuren. Frå no av betyr alle symbola verdiane av vektorane. Så v betyr | v | osv. Likeforma trekantar gir oss då at

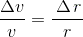
Δr er tilnærma lik buelengden som vi kan skriva v Δt, der Δt er tida det tar mellom dei to punkta:

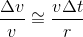
Når vi ordnar på denne likninga får vi:

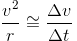
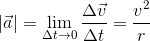
Dermed har vi vist formelen for akselerasjonen til ein gjenstand som går i sirkel med konstant banefart. Dette kallar vi for sentripetalakselerasjon:

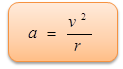
Retningen til a

Når vi lar Δt gå mot null, vil vektoren r₂ bli meir og meir lik r₁. Vi får då ein likebeina trekant med spissare og spissare vinkel, og det betyr at vinkelen mellom v og Δv vil gå mot 180°/2 = 90°. Altså vil Δv , og derfor også a, stå normalt på v. Samtidig veit vi at v også står normalt på r, så må a og r vera parallelle. Og sidan v₁ alltid ligg over v₂, så må retningen vera inn mot sentrum av sirkelen.

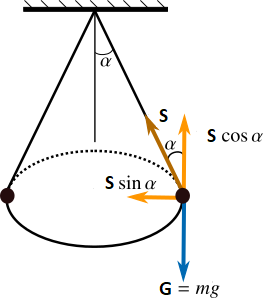
Vi gjentar dette: Retningen til akselerasjonen er alltid retta inn mot sentrum når vi har sirkelbevegelse med konstant banefart. Det er også viktig å forstå at farten (som vektor) ikkje er konstant, men absoluttverdien av denne vektoren, er det! Og det er dette vi kallar for banefarten. Eksempel på dette er (tilnærma) planetbevegelsar, og kjeglependel (konisk pendel). Det første er eit eksempel på bevegelse der bare ei kraft virkar, nemlig gravitasjonskrafta. Vi veit at denne krefta virkar inn mot sentrum av sola, og har derfor same retning som akselerasjonen. Og slik må det jo vera, sidan Newtons andre lov seier at akselerasjonen har same retning som kraftsummen. I ein kjeglependel er det derimot to krefter som virkar (når vi ser bort frå friksjon og luftmotstand) Det er snorkrafta  S, og tyngdekrafta G. (Sjå figuren under). Vi har ingen bevegelse i vertikal retning, så den vertikale komponenten av S, som er lik  S cos α må vera lik og motsatt retta av G, slik at disse opphever kvarandre. Derfor blir kraftsummen i dette tilfellet lik S sin α, som er retta innover mot sentrum.

Andre eksempel på slik bevegelse er ein bil som kjører med konstant fart i ein sving, eller eit fly som flyr i ein sirkel med konstant fart.

Når banefarten ikkje er konstant:

I ein krumlinja bane er fartsvektoren alltid parallell med tangenten til banen. Men når banefarten ikkje er konstant, kan akselerasjonsvektoren kan ha mange ulike retningar. Akselerasjonen til ein planpendel i ulike posisjonar kan for eksempel sjå slik ut:

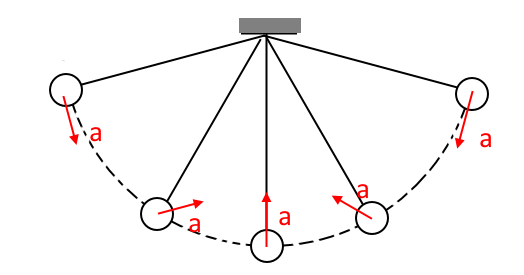
Korfor blir det slik? Vi kan dekomponera akselerasjonsvektoren i ein normalkomponent a_n og ein tangentiell komponent a_t. dvs slik at totalvektoren a er ein vektorsum av disse: a = a_n + a_t.

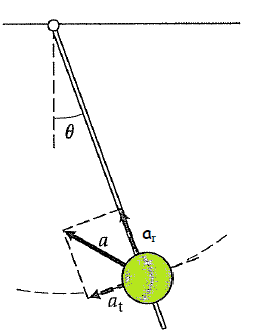
Den tangentielle komponenten er rett og slett den deriverte av banefarten. a_t = v'(t), og tilsvarar vanlig akselerasjon for rettlinja bevegelse. Normalkomponenten er sentripetalakselerasjonen som gitt ved formelen vår. Når farten er konstant, så er v'(t) = 0, og akselerasjonen er lik sentripetalakselerasjonen, slik vi har sett over.

Dette er ikkje tilfelle med ein planpendel, for der er banefarten null i ytterpunkta, og så aukar den nedover inntil den når max i loddrett posisjon, for så å minka oppover til motsatt endepunkt. Dette betyr at i ytterposisjonen vil akselerasjonen vera reint tangentiell. I mellomposisjonen har vi ein mix av begge deler. Pendelen har fått opp farten, og vi har derfor ein sentripetalkomponent. Samtidig har vi fremdeles auke i banefarten, slik at der også er ein tangentiell komponent. I bunnpunktet er farten på det høgaste. Det betyr at vi har ingen auke i banefarten akkurat der, så då er det kun sentripetalakselerasjonen som gjeld.

Eit eksempel på dette er loop i berg-og-dalbane der banefarten jo ikkje er konstant. Det medfører at vi også her har ein tangentiell komponent. Men i to punkt i banen vil v'(t) vera null, nemlig i bunnen og i toppen av banen. Andre eksempel er bilkjøring og skikjøring over ein sirkelforma bakketopp.

LENKER

Deriving the centripetal acceleration formula.

Fifth Gear Loop the Loop. Video med ein bil som kjører i loop.