Badevaktproblemet
Den store fysikaren Richard Feynman hadde ein gong ei forelesing om optikk (korfor den handla om det, vil bli klart seinare) der han presenterte det som er blitt kjent som badevaktproblemet (Lifeguard problem). Det går ut på å finna den fortaste veien mellom ein badevakt og ein person som treng hjelp. Som han sa: "Let us imagine that a beautiful girl has fallen out of a boat, and she is screaming for help in the water at point B." Vi kan jo lura på om han meinte at det var relevant at det var ei "beautiful girl" (Feynman skal ha vore litt av ein skjørtejeger), men problemet vi skal løysa, er uansett å finna den veien som tar kortast tid.
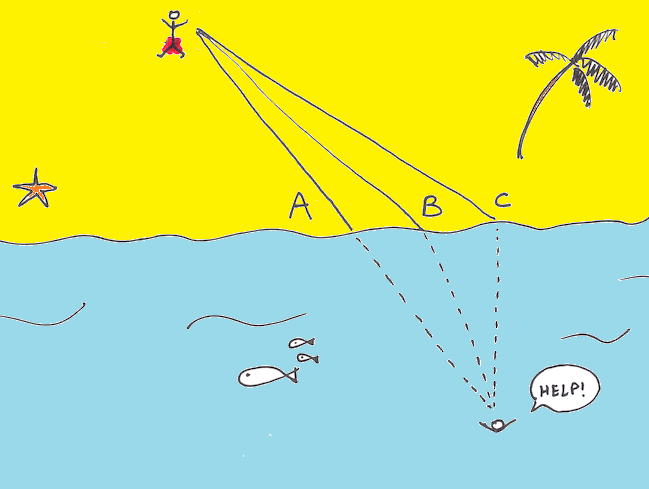
Mange vil jo gjetta på at det er den rette linja (linje A) som er fortast. Men det som gjer problemet litt vanskelig er at farten til badevakten er ganske så forskjellig på land og i sjøen. La oss anta at badevakten er ganske sprek, slik at farten på land er 8 m/s og i vatnet 2 m/s. Då virkar det logisk at han bør springa litt lenger langs land før han legg på svøm. Spørsmålet er kor langt? Skal han ta rute B, eller rute C, eller noko i mellom?
Vi kan rekna på dette, men då må vi også kjenna posisjonane til badevakten og personen i vatnet. Så la oss anta at avstanden frå badevakten (i punkt P1) til vannkanten er femti meter, og det same med personen i vatnet (i punkt P2). Dermed er det 100m i y-retning mellom dei. Så kan vi la avstanden mellom dei to i x-retning også vera 100 meter. Dermed kan vi tegna problemet (pluss eit forslag til løysing) som på figuren under.
Hvis vi veit kor badevakten går uti, så er det ikkje vanskelig å rekna ut kor lang tid han brukar. Så la oss bare tippa at det skjer i punktet X = (70,50). Dette er altså vårt første forslag, og vi vil no rekna ut kor lang tid det tar for badevakten langs denne ruta. Han eller ho skal altså i dette tilfellet først springa frå P1 til X og deretter sømja så fort som mulig frå X til P2. Begge disse etappane er hypotenusen i kvar sin rettvinkla trekant som skissert på figuren, og då kan vi bruka Pytagoras: Den øverste trekanten har katetane 50m og 70m, og då finn vi at badevakten må springa distansen d1 = 86.02 m. Han bruker dermed tida t1 = 86.02 / 8 = 10.75s på dette stykket. Deretter må han sømja distansen d2 = 58.31 m, (katetar 50m og 30m) og bruker då tida t2 = 58.31 / 2 = 29.16. Tilsaman har badevakten altså brukt tida 86.02 / 8 + 58.31 / 2 = 39.91 s .
Men vi trur at han kan gjera betre enn som så, så vi vil vil rekna ut (nesten) alle tidene for alle mulige krysningspunkt X, og deretter finna den minste tida. I verkeligheten kan vi ikkje rekna ut alle, men vi kan gjera eit estimat ved å rekna ut for kvar cm bortover langs x-aksen. Då får vi 10000 punkt å rekna ut tider for, men det går jo fort med datamaskin. Vi kallar altså x-koordinaten til X (originalt nok) for x. I eksempelet over hadde vi x = 70. Den gjenståande avstanden i x-retning blir då 100 - x. Katetane i den øverste trekanten har altså sidene 50m og x, og den nederste har 50m og 100 - x. Vi kan derfor setja opp eit uttrykk for tida som funksjon av x, slik:
Grafen til denne funksjonen ser slik ut:
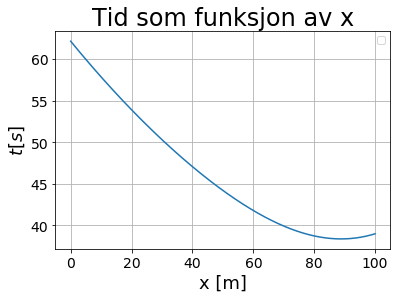
Vi ser at grafen har eit minimum i nærheten av 90. Dette kan vi finna numerisk, ved å rett og slett finna den minste av alle dei 10 000 tidene vi har rekna ut. Dette kallast ofte for Brute Force-metoden Men vi kan også bruka ein annan optimaliseringsalgoritme, for eksempel Equal Interval Search Method. Uansett finn vi at den kortaste tida er for x = 88.84. Altså må badevakten ganske langt til høgre før han eller ho går ut i vatnet:
Snells brytningslov.
No har vi funne svaret, men vi skal gå vidare. For det viser seg at badevakten vår føljer ei tilsvarande rute som lyset gjer når det går frå eit medium til eit anna. Så badevaktproblemet handlar egentlig om optikk! Vi kan tenkja oss at lyset går frå P1 som befinn seg i luft, og til punkt P2, som befinn seg i glas. På figuren over har vi også vist det som vi i optikk og bølgelære kallar innfallsloddet. Dette er den stipla linja som står normalt på grenseflata (dvs. strandlinja i vårt tilfelle). Vi har også vist vinklane som dei to linjene P1X og XP2 har i forhold til innfallsloddet. Vi kallar vinkel θ1 for innfallsvinkelen og vinkel θ2 for brytningsvinkelen. La oss no rekna ut sinus til disse vinklane og dividera med fartane på dei respektive sida. På oversida får vi sin(60.63) / 8 = 0.11 og på undersida får vi sin(12.58) / 2 = 0.11, med andre ord: vi får same svar. Vi har altså at:
sin θ1/ v1 = sin θ2 / v2
Og dette er ikkje tilfeldig. Du kan sjøl prøva å variera både fartane og geometrien i dette problemet, og rekna ut ny verdi for vinklane, og du vil sjå at dette alltid stemmer. Dette er kjent som Snells brytningslov. Som regel vil du finna loven skrive på ein annan måte. Hvis vi innfører dei nye variablane (som kallast for brytningsindeksane) n1 = c/v1 og n2 = c/v2, så kan vi skriva likninga om til: n1 sin θ1 = n2 sin θ2 .
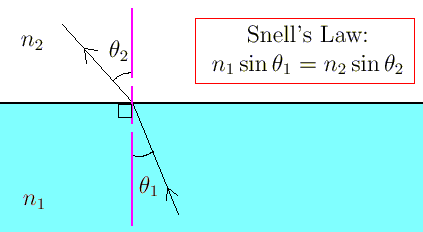
Fermats prinsipp.
Men kva er det egentlig som har skjedd her? Vi tok jo utgangspunkt i det som var eit mekanisk / praktisk problem og endte opp med Snells brytningslov som gjeld for brytning av bølgjer som går frå eit medium til eit anna. Betyr dette at lyset følgjer den snaraste veien? Ja, faktisk. Dette kallast Fermats prinsipp, etter den berømte Pierre de Fermat. Dette prinsippet har blitt generalisert til noko som kallast virkningsprinsippet, som først fekk ein djupare forklaring med kvantemekanikken. Og nettopp vår venn Feynman var ein av dei fremste som bidrog.Så eg legg ut ei lenke til hans forelesing ein gong til, så kan du sjå korleis ein av fysikkens kjappaste hjernar forklarte dette.
LENKER
Simple proof for Snell's law of refraction. (Både geometrisk og basert på Fermats prinsipp)
To Save Drowning People, Ask Yourself “What Would Light Do?
Fermat’s Principle and the Laws of Reflection and Refraction.
