Populasjonsdynamikk handlar om å simulera utviklinga av antal dyr i ein eller fleire dyrepopulasjonar. Vi skal sjå på fem modellar for dette. Dei tre første handlar om korleis ein enkelt art vil utvikla seg uavhengig av andre, og i dei to siste eksempela ser vi på to ulike artar som påvirkar kvarandre. Felles for alle disse modellane er at dei er alt for enkle til å vera realistiske simuleringer av verkelige bestandar. Men vi kan læra litt om korleis populasjonen til artar som lever isolert kan utvikla seg, og korleis bestandane til to ulike artar som er avhengige av kvarandre kan utvikla seg.
Ein bruker ofte variabelen N for antalet dyr i populasjonen. (har brukt liten n i program, for å skilja frå stor N, som fremdeles er antal iterasjonar.) N er ein funksjon av tid. N' er den deriverte av denne funksjonen, og fortel korleis antalet dyr endrar seg per tid. I alle modellane her, set vi opp ein differensiallikning (difflikning) der N' er gitt ved eit uttrykk.
Dei modellane vi skal sjå på er:
Her modellerer vi ein populasjon som ikkje har begrensningar i forhold til mat osv. Ein veldig enkel modell kan då beskrivast med difflikninga
N' = r*N
Det betyr at endringa i populasjonen er proporsjonal med populasjonen sjøl. Begrunnelsen for denne er at vi tenkjer at uten begrensningar så vil ein viss prosent av dyra få barn i løpet av ein periode, mens ein viss prosent vil dø. Under optimale forhold vil fødselsraten vera større enn dødsraten, slik at differansen r, som vi kallar reproduksjonsraten, vil vera positiv, og konstant.
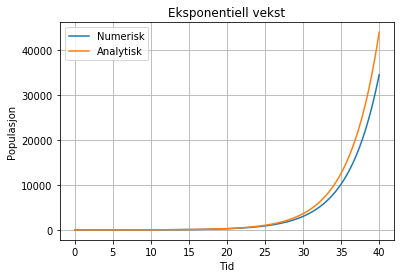
Denne likninga kan løysast eksakt, og svaret er N(t) = N0*e(rt). Dette kallast for den analytiske løysinga, og kurven (oransje) ser slik ut:

Denne grafen kallast ofte for ein J-kurve, pga formen. Her har vi også
løyst likninga numerisk (blå kurve). Sjå Pythonkode
her. Merk at vi kan få den numeriske løysinga veldig nær den
analytiske, når vi reknar med små nok tidssteg. I modell 2 blir også både
ein numerisk og den analytiske løysinga vist, mens i dei tre siste
modellane er det bare numeriske løysingar.
Problemet med den eksponentielle veksten er at den aukar i det uendelige, og i verkeligheten vil ein slik bestand bruka opp alle tilgjengelige ressursar. Då vil dyra konkurrera om dei begrensa ressursane. Når individ innan same art konkurrerer, kallast det for intraspesifikk konkurranse. Effekten av dette er at veksten etter kvart avtar. Dyra blir ikkje så gamle, og mange vil ikkje rekka å få avkom. Det betyr at når populasjonen er for stor, så vil det dø fleire dyr enn det blir født. Ein meir realistisk modell får vi derfor når vi antar at det fins eit bærekraftig nivå, B, for bestanden, som fortel om det maksimale antalet dyr som kan leva der uten at populasjonen skal begynna å minka igjen. Då bruker vi difflikninga:
N' = r*(B-N)/B *N
Logikken her er at vi erstattar konstanten r med ein variabel som er lik den gamle multiplisert med faktoren (B-N)/B. Når N er liten blir denne tilnærma lik B/B, dvs 1. Vi får då (nesten) eksponentiell vekst i begynnelsen. Men etter kvart som populasjonen, dvs N, aukar, vil faktoren nærma seg null, og veksten vil dermed avta. Når N er tilnærma lik B, så vil veksten stoppa heilt opp. Vi får då ei utflating av kurven:
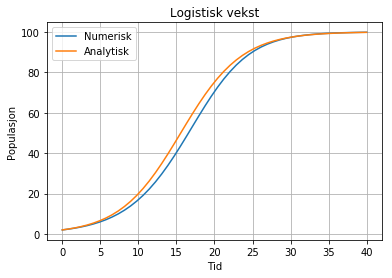
Denne grafen kallast ofte for ein S-kurve. Sjå Pythonkode her.
Men heller ikkje denne modellen fangar opp dynamikken for ein enkeltståande art. Mange arter formeirer seg så fort at dei ikkje rekk å tilpassa seg minkande ressursar. Det medfører at antalet kan bli større enn det bærekraftige nivået. Deretter vil populasjonen få ein negativ korreksjon som tvingar den under bærekraftig nivå igjen. Dette kan vi modellera med å innføra ein forsinkelse. Hvis vi lar N i faktoren (B-N)/B, vera populasjonen sin størrelse for ei tid tilbake. Her må vi skriva N fullt ut, altså som ein funksjon av t. Hvis vi lar forsinkelsen vera τ, så kan vi setja opp følgande difflikning:
N'(t) + r*(B - N(t - τ))/ B*N(t)
No kan kurven sjå ut som under. Her er den orange grafen den same som over, og forsinkelsen τ = 20.
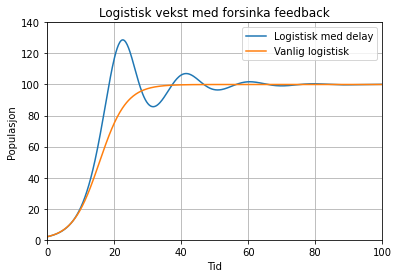
I dette eksempelet ser vi at i begynnelsen veks populasjonen fort, og havnar over bærekraftnivået fordi den endå ikkje har "møtt veggen". Men når den først møter veggen i form av alt for lite mat, vil den svinga ned i gjen, før den til slutt legg seg på nivået. Men hvis den første toppen er veldig høg (ofte kalla overshoot) så vil også reaksjonen bli meir alvorlig, og i verste fall kan bestanden bruka opp alle sine ressursar og då kan den kollapsa fullstendig. Ein annan effekt av overforbruk av ressursane er at også det bærekraftige nivået kan bli redusert. For eksempel kan overutnytting av jordsmonn kan resultera i erosjon og tap av jord, og redusert produksjon, sidan det tar veldig lang tid å regenerera topplaget av jord, der vi kan dyrka mat.
Men så er det jo slik at ingen art lever fullstendig isolert frå andre artar. Disse enkle modellane med eksponentiell og logistisk vekst tar ikkje høyde for at artar kan konkurrera med andre om ressursar, hjelpa kvarandre eller drepa / leva av kvarandre, og i det heile påvirka kvarandre på mange ulike måtar. Vi skal sjå på to eksempel. Når nisjene til to artar overlappar, oppstår det konkurranse mellom artane (såkalt interspesifikk konkurranse). Dette skjer altså når dei to artane delvis lever av dei same ressursane i same området. Men hvis den eine arten lever av den andre oppstår eit Predator-bytte-forhold. I begge disse typane er det konkurranse. Hvis den eine arten forsvinn, så vil den andre gjera det betre (dette gjeld bare for fisken i fisk-hai eksempelet under. Haien vil sjølsagt dø uten fisk!) Men det fins også samspel som den eine eller begge partane kan tena på. Når to ulike artar lever saman i ein tett relasjon over lang tid, kallar vi det symbiose. Hvis begge partar tener på dette, kallast det for mutualisme. Når den eine parten tener på den, mens den andre er stort sett uberør, kallast det kommensalisme, Men når den eine parten tener på det, mens det er til skade for den andre, snakkar vi om parasittisme. Det fins også former for mutualisme som ikkje er symbiotiske. Sjøl om alle disse samarbeidsformene er interessante og viktige i naturen, så skal vi ikkje sjå på dei her.
Her har vi to litt kompliserte difflikningar som styrer utviklinga av art 1 og 2.
N1' = r1*N1(1 - α11*N1 - α12*N2)
N2' = r2*N2 (1 - α21*N2 - α22*N1)
Her er
Bytt om 1 og 2, så har du forklaring på α21 og α22.
Sameksistens mellom to konkurrerande artar kan forekomma hvis α11 > α12 og α22 > α21. Det kan vi oversetja til at sameksistens opptrer når effekten frå kvar art på seg sjøl er større enn effekten på konkurrenten. Hvis ikkje vil den eine arten utkonkurrera den andre.
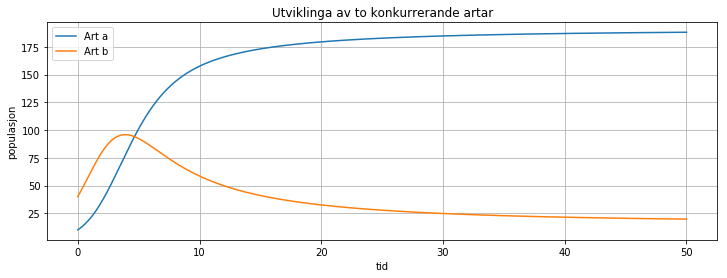
Når to artar delvis lever av dei same ressursane vil resultatet vera at dei stabiliserer seg på eit lavare nivå enn det dei ville vore på uten konkurranse. Og, som vi ser i eksempelet, er det ikkje gitt at det er den arten som har størst populasjon i utgangspunktet som endar opp med størst antal. Men det kjem gjerne ikkje som nokon overraskelse at hvis alle parameterane er like for dei to artane, så er dei i denne samanhengen like artar, og då vil begge kurvene vera like og sjå ut som ein vanlig logistisk funksjon.
I eksempel 1,2 og 3, er den deriverte av bestanden bare ein funksjon bare av bestanden sjøl. Men når ein art lever av ein annan, så vil den deriverte av bestanden også vera avhengig av den andre. Vi ser på eit enkelt eksempel med fisk og hai. Ein klassisk måte å modellera dette på, er å bruka dei såkalte Lotka-Volterra-likningane. I vårt eksempel ser dei slik ut:
Fisk: F' = αH - βFH
Hai: H' = δGH - γH
I likninga for fisken fortel det første leddet på høgre sida at fisken
har ein tendens til å auka proporsjonalt med antallet. Men no kjem det eit
ekstra ledd som fortel at den også har ein tendens til å minka
proporsjonalt med produktet av antalet fisk og antalet hai. Likninga for
hai, seier at ein tendens er at antalet derimot aukar proporsjonalt med
produktet av antalet fisk og antalet hai. For det er jo haien som lever av
fisken. Men vi har også eit ledd som seier at antalet hai vil gå ned
proporsjonalt med antalet hai. Dette er dødsraten til haien. Eit viss
prosent av haien dør per tid. Men då kan vi jo spørja oss korfor det ikkje
er eit slikt ledd for fisken? Svaret er at parameteren α er ein
netto-faktor som kombinerer fødselsrate og dødsrate. Vi kunne hatt eit
ledd k1*H som tel positivt (fødsel) og eit ledd - k2*H som er negativt
(død). Men vi slår disse saman til eit ledd αH der α = k1 - k2.
Når vi simulerer dette systemet, kan det sjå slik ut:
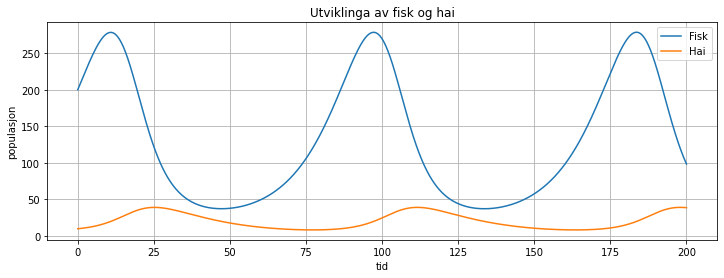
Vi ser at haibestanden er lav i starten, og derfor kan fisken formeira seg raskt. Men straks haibestanden begynner å ta seg opp, vil den redusera veksten i fiskebestanden. Når fiskebestanden begynner å gå nedover, er resultatet at også haibestanden vil begynna å gå ned, sidan det blir mindre mat. Det betyr i sin tur at fiskebestanden kan ta seg opp igjen når haibestanden er lav. Og slik fortset dei to bestandane i syklusar med høge og lave antal, men som vi ser, har haibestanden sin topp litt seinare enn fiskebestanden.
Ein kan også modellera ein planteetar (feks kyr) og maten (feks gras) som
ein variant av predator-bytte-modellen. Då kan det sjå slik ut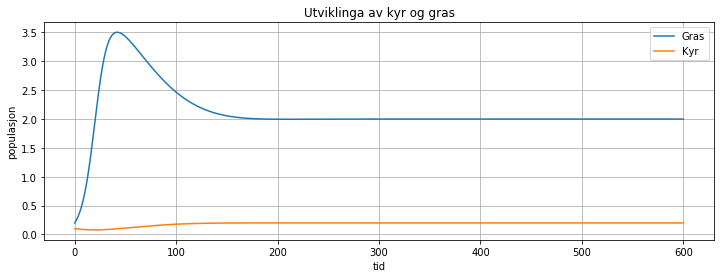
Her ser vi at så lenge antalet kyr er lavt, så veks graset friskt, men etter kvart som det blir fleire kyr, så minkar det litt på graset, inntil begge populasjonane legg seg på eit bærekraftig nivå.
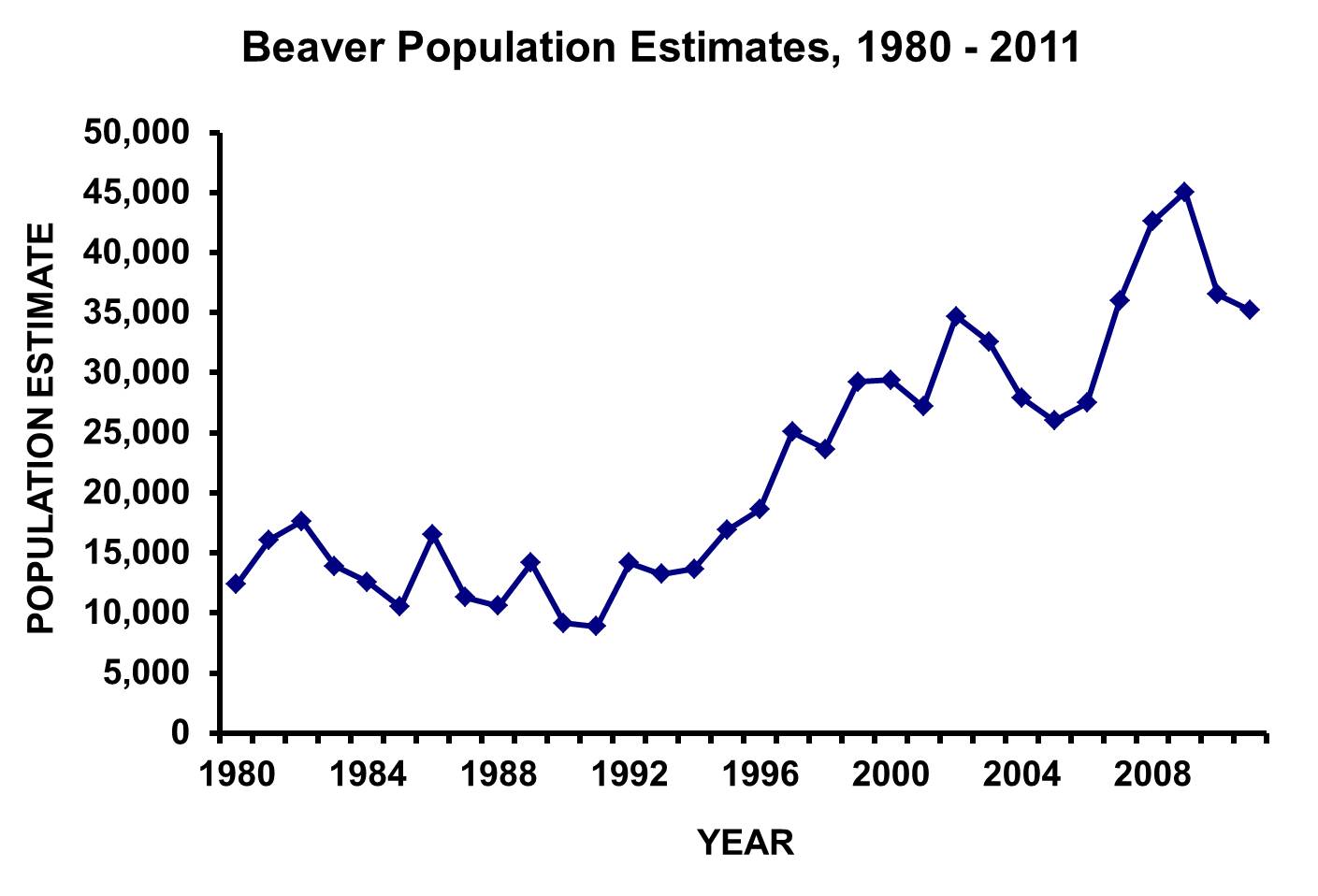
I verkeligheten ser grafane ikkje slik ut som vi har sett over. Ein verkelig bestand vil vera avhengig av veldig mange variable, som tilgangen på mat, konkurranse med andre artar om maten og om dei blir jakta på av andre dyreartar eller mennersker. Så er det andre faktorar som klima, forurensing mm, som har betydning for levekåra. Alt dette betyr at ein populasjon vil variera på ein meir uregelmessig og uforutsigbar måte. Eksempelet under viser estimater for den amerikanske beveren (henta frå Ohio Department of Natural Recources). Vi ser både ein svingning med ein periode på to-tre år, men også ein endring som går over heile perioden. Eg vil ikkje prøva på å forklara denne grafen, men hvis vi skulle komma i nærheten av å modellera dette, så må vi ta med veldig mange fleire parameterar, både som gjeld miljøet (temperatur, saltholdighet, forurensing mm. som gjeld jord, vatn og luft) og som gjeld mange andre artar som lever i miljøet, inkludert mennesket.
.
Til slutt noken ord som såkalte agentbaserte modellar, også kalla individbaserte modellar (IBM). Alle modellane vi har sett på til no, simulerer på populasjonsnivå. Det vil sei at dei bare ser på antalet dyr innanfor ulike artar, og antar at alle dyr innan ein art er like, eller i alle fall at vi kan sjå bort frå ulikhetene. Det er heller ingen uliheter i levekår osv. Men det går an å tenkja på ein annan måte. Vi kan simulera kvart dyr og kvar plante individuelt. I ein slik modell kan ein plassera ut planter og dyr i ein geometrisk modell (feks. ei slags matrise) der dyr kan bevega seg. Planter veks i tomme celler, planteetarar forsyner seg av disse når dei havnar på ei celle med ei plante, men kan også bli eten av ein kjøttetar som dukkar opp. Her kan vi tenkja oss at egenskapane til dei ulike dyra er forskjellige, og vi kan tenkja oss at levekåra i dei ulilke "cellene" er forskjellige, osv. Eit tidsbilde kan sjå slik ut: (Figurane under er henta frå boka The computational Beauty of Nature av Gary William Flake.)
Figuren over viser eit agentbasert økosystem med tre artar: ei plante, ein planteetar og ein kjøttetar (predator)
Algoritmen i eit agentbasert modell har ein logikk som beskriv tilstandane til dyra og plantene, og kva som kan skje i denne virtuelle verda. Dei må beskriva hendelsar som at ein dyr et ei plante. I tillegg til å fjerna planta, så vil også energien til dyret auka. Med andre ord må vi vita ikkje bare posisjonen til kvart dyr, men også energien, og evt. også andre parameterar, som alder, eller om individet er gravid mm. Kvart individ er med andre ord unikt i den forstand at dei har forskjellige tilstandar. Når eit dyr ikkje et vil energien minka gradvis, og når den er brukt opp dør dyret, dvs. det blir tatt ut. Algoritmen må også ha reglar for bevegelse (som er delvis tilfeldig) og for fødsel av eit nytt dyr. Ein kan tenkja seg å ta med andre hendelsar og tilstandar og til og med evolusjon i slike modellar.
Når ein kjører ein agentbasert modell, kan resultatet bli som under. Det interessante er at i denne modellen er det ingen difflikningar og ingen parameterar for bærekraft osb. Likevel får vi kurver som liknar dei vi har sett før. Bærekraft viser seg her som ein effekt (såkalt emergent egenskap) av at det er konkurranse om begrensa ressursar i modellen. Svingningane er ein effekt av samspelet mellom artane, mens dei ujevne kurvene nok er ein effekt av tilfeldige hendelsar.
Populasjonsutvikling i ein individbasert modell. Dette er resultatet av ei simulering i C, henta frå boka over. Du kan finna kjeldekoden her.
NDLA: Populasjonsvekst. Logistisk vekst, Vekst i populasjoner og Proporsjonal vekst.
Exponential & logistic growth Khan Academy
Types/Terms describing Interspecific Interactions. Grei oppsummering
Species Interactions and Competition.
Dynamics of a plant–herbivore model with differential–difference equations.
Intro to individual-based models (IBM). er del av et kurs.
Critical thresholds in sea lice epidemics: evidence, sensitivity and subcritical estimation. Ref Therese
Dynamics of a plant–herbivore model with differential–difference equations.